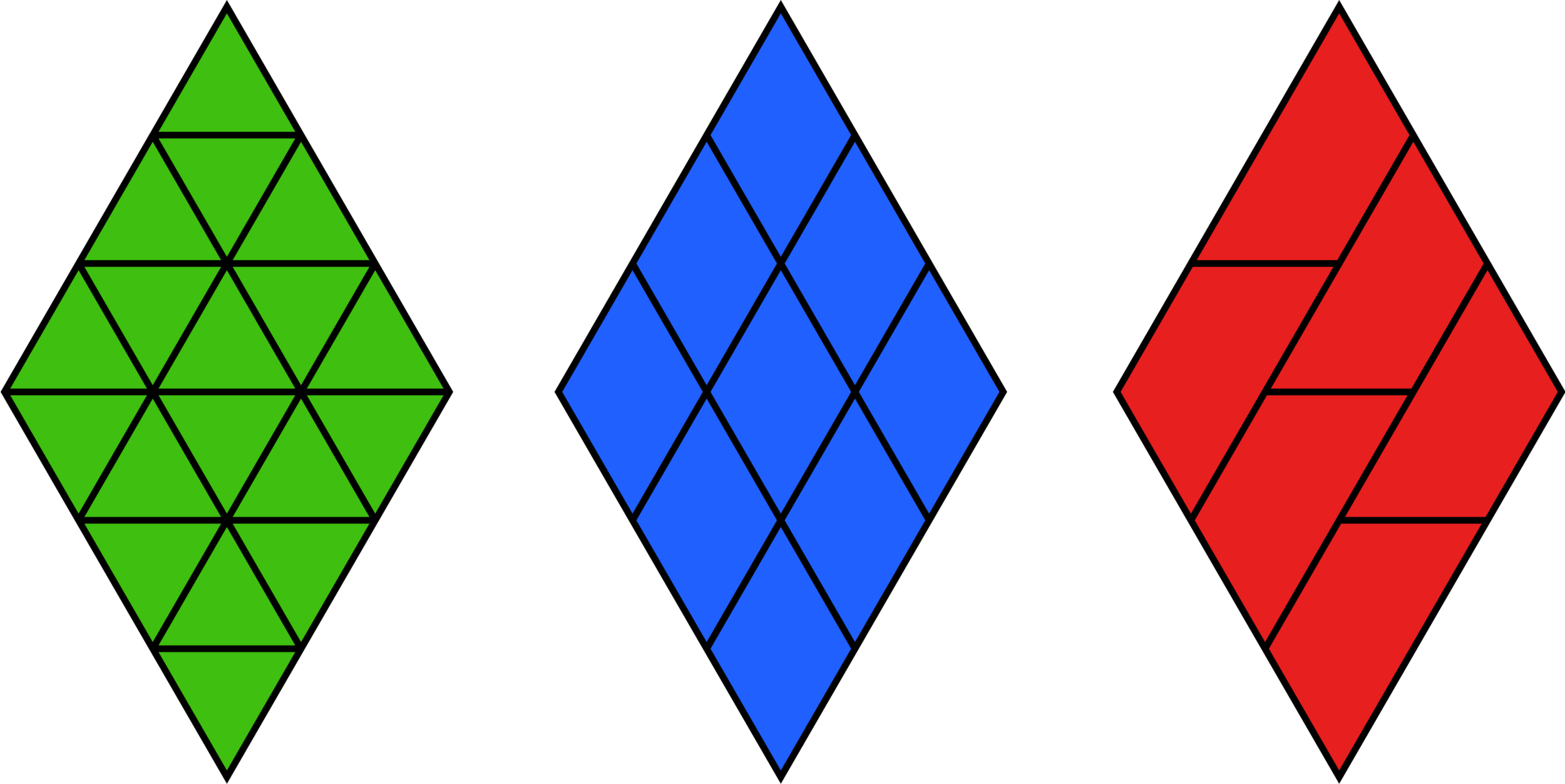
One Type Tiling
How it works
Given a shape, can you fit pattern blocks together to tile that shape (that is, to cover it completely without going over the edge) if you’re only allowed to use one type of pattern block? Which types of block work, and which don't? For the types of block that work, how many copies of the block do you need in order to tile the shape?
In this activity, students try to tile 2x and 3x versions of the basic pattern block shapes. First, they try to do this using only copies of the pattern block that corresponds to the shape being tiled (for example, using only green triangles to tile scaled-up versions of green triangles). Next, they try to do this using copies of pattern blocks that don’t match the shape being tiled (for example, using only green triangles to tile scaled-up versions of blue rhombi). In each case, when it is possible to tile the shape, students count how many blocks they used, and they notice some interesting patterns.
Self-Tiling Data Recording handout
One Type Tiling Data Recording handout
Why we like this activity
- It’s fun! Students enjoy tiling with the pattern blocks and figuring out how many copies of different types of blocks they need in order to tile various shapes.
- It helps students develop spatial reasoning.
- It helps to develop numerical reasoning.
It requires students to engage in mathematical habits of mind:
Finding and using strategies to tile different shapes.
Using logic / looking for patterns / finding strategies / making and testing predictions / understanding and explaining when exploring how many copies of a specific type of pattern block it takes to tile the shapes.
- It has a low floor and a high ceiling: Students can start tiling by trial and error, but there’s a lot to discover and figure out about how many blocks of each type it takes to tile shapes of different sizes.