Jumping Beans
How it works
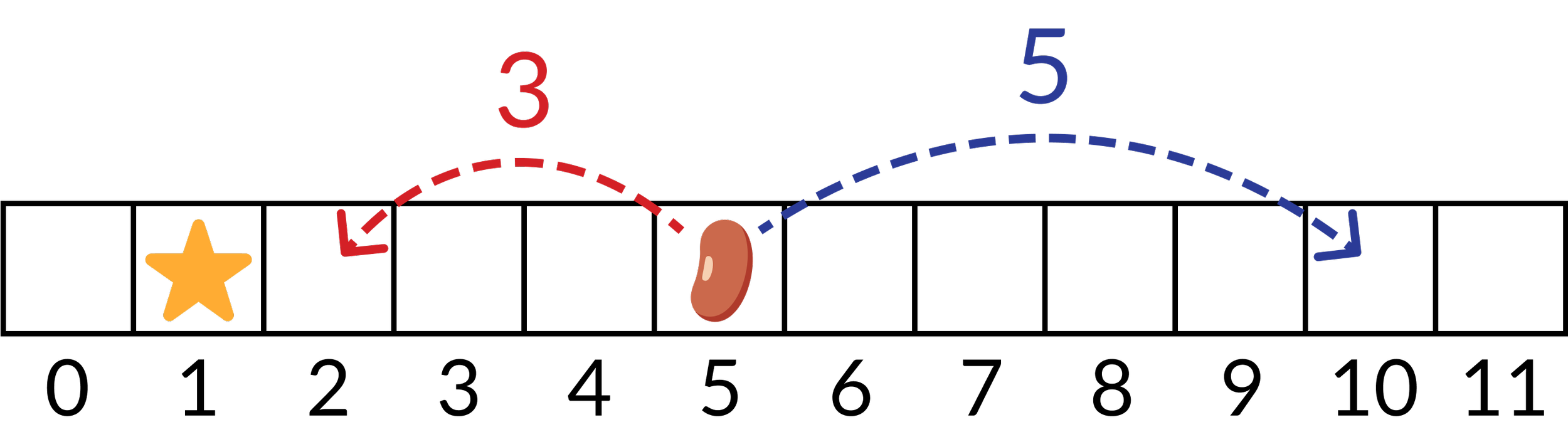
Imagine that you have a row of squares, labeled 0 through 20 from left to right, and you have a jumping bean that starts in square 0.
The goal is to get the bean into square 1.
However, there are only 2 types of jumps the bean can make: The bean can only jump 5 squares to the right or 3 squares to the left.
Is it possible to get the bean into square 1 using only these jumps? If not, what is the square with the smallest number (bigger than 0) we can reach? What if the bean can only jump 6 squares to the right or 3 squares to the left? What about with other pairs of jumps?
In this activity, students explore a variety of different pairs of jumps. They discover that it's possible to get the bean into square 1 for some pairs of jumps but not for others. They develop strategies for getting the bean into square 1 when it's possible, and try to predict whether or not it will be possible to get the bean into square 1 based on the jump sizes.
Why we like this activity
It’s fun! Students enjoy trying to get the bean into square 1 and trying to predict whether or not it will be possible.
It helps students develop algorithmic reasoning.
It helps students develop numerical reasoning.
It requires students to engage in mathematical habits of mind:
Finding and using strategies when trying to get the bean into square 1.
Using logic and understanding and explaining when trying to determine whether or not it's possible to get the bean into square 1 with a given pair of jumps
Looking for patterns and making and testing predictions when trying to predict whether or not it's possible to get the bean into square 1 with a given pair of jumps.
It has a low floor and a high ceiling: Students can get started moving the bean by trial and error, but more complex challenges require more careful strategizing, and there are some interesting patterns to discover!